Конспект урока по математике 3 класс

Предмет: математика.
УМК: Перспектива.
Класс: 3.
Тема урока: Как люди научились считать.
Тип урока: изучение нового материала.
Технология занятия: проблемно-диалоговая.
Цель: рассмотреть историю возникновения чисел,
Задачи:
• Образовательная: познакомится с историей возникновения чисел, продолжить совершенствовать математические навыки и математическую речь.
• Развивающая: продолжить развивать логическое мышление, память, внимание, математическую речь.
• Воспитательная: продолжить воспитание интереса к математике, уважение к мнению товарищей.
Оборудование: учебник математики 3 класс Л.Г. Петерсон 2014г., презентация, видео с физминуткой, карточки с опроными словами, мультимедийная доска, проектор, компьютер, колонки.
Универсальные учебные действия.
1.Личностные:
• умение признавать собственные ошибки;
• формирование ценностных ориентаций;
• формирование математической компетентности.
2.Регулятивные:
• учитывать ориентиры, данные учителем, при освоении нового учебного материала;
• проверять результаты вычислений;
• адекватно воспринимать указания на ошибки и исправлять найденные ошибки;
• оценивать собственные успехи в вычислительной деятельности.
3. Познавательные:
• анализировать условие задачи;
• осуществлять синтез условия текстовой задачи;
4. Коммуникативные:
• задавать вопросы с целью получения нужной информации;
• высказывать свое мнение при обсуждении задания.1.Организация начала занятия.
Здравствуйте,садитесь.
Звонок веселый прозвенел
Он заниматься нам велел
Долгожданный дан звонок,
Начинается урок.
Ум и сердце в работу вложи,
Каждой секундой в труде дорожи.
2.Минутка чистописания.
Отступите от классной работы вниз одну клетку и пропишите строчку чисел, которые делятся на 3 последнее число у вас будет 30. Кто справился сигнал. Какие числа вы записали?
3.Устный счет.
Посмотрите на слайд, нам нужно будет решить круговые примеры. Ответ примера соответствует началу следующего. 82:2. Сколько будет?(41) (появляется на слайде правильный ответ)Значит, какой следующий пример. (аналогичная работа со всеми примерами)
Посмотрите на слайд, составьте по данным выражениям задачи. Пусть 80 это яблони, а 2 это сливовые деревья. Давайте составим задачу к первой схеме. Кто придумал сигнал. Сколько получится в ответе. (аналогичная работа со остальными схемами ).
А сейчас мы с вами вспомним тему множества. Посмотрите на множество. Пусть А- множество детей, В- множество изучающих английский, С- изучающих французский, D- множество парт, Е – ходят на английский и французский. Найдите множества: А, В, С, D, Е. Что обозначают закрашенные множества.
Сейчас мы проведем блиц-опрос. Вы должны ответить на вопрос и доказать свое мнение. Кто знает ответ, поднимает руку. Сколько ног у 8 слонов?(32) Как вы это узнали? Сколько рогов у 9 коровах? (18) Сколько хвостов у 6 ослов? (6) У одного ребенка – три котенка. Сколько будет котят у трех ребят?(9) Сколько пальчиков у семи мальчиков? (70)
Что бы узнать, что мы сегодня будем изучать на уроке мы заглянем в волшебный сундучок. (вытаскиваются из сундучка листочки с названием тем, которые крепятся на доску) Сегодня мы познакомимся с системой счисления, первыми цифрами , открытием нуля и ответим на вопрос существует ли самое большое натуральное число? А познакомимся мы в начале с системой счисления.
4.Изучение нового материала.
Раньше людям приходилось считать на пальцах. Чтобы посчитать большое количество предметов, к счету привлекали много людей. Один считал единицы, второй-десятки, третий- сотни. Давайте и мы попробуем, так посчитать. (к доске выходят 3 человека 1ученик-единицы, 2- десятки, 3- сотни)В руках у меня 1 ручка покажите, как люди загибали пальцы. А теперь у меня их 10 и как только единиц становилось 10, то человек, который показывал десятки загибал палец. Покажите как это. Как только десятков становилось 10, что делал человек, который показывал сотни? (загибал 1 палец). Спасибо, ребята садитесь. Такой счет лег в основу систему счисления, принятой почти у всех народов мира. Она называется дисятичной (вывешивается слово на доске)системой. Ребята, а удобно было ли изображать на пальцах числа? (нет) У некоторых народов до сих пор сохранились, такие системы счисления, как пятеричная, двадцатиричная(вывешивается слово на доске). Самой серьезной соперницей дисятичной системы оказалась двенадцатиричная(вывешивается слово на доске). Вместо десятков применяли при счете дюжины(вывешивается слово на доске), то есть группы из 12 предметов. Даже в современное время продают, некоторые товары дюжинами, например наборы столовых предметов.
Папуасы считали все парами, но именно их двоичная(вывешивается слово на доске) система счисления оказалась самой полезной для современной техники, так как на основе двоичной системы счисления работают современные компьютеры.
Долгое время после того, как появились название чисел, люди их не записывали, потому что не умели писать. Они прибегали к зарубкам на дереве или на кости, к узелкам на верёвках, рисунках на мягкой глине и многое другое.
Такие знаки уже нельзя было перекладывать с места на место, убирать одни и добавлять другие. Вместо этого приходилось думать, мысленно выполнять операции над знаками. Немало различных способов записи чисел было создано людьми. В Древней Руси числа обозначались буквами с особым знаком-титло,(вывешиваются на доске) который писали над буквой.
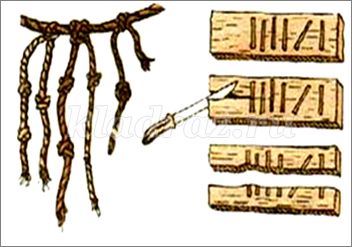
Всем известны римские цифры, которые употреблялись в Древнем Риме более 2500 лет назад.
Расшифруйте, какое число записано у меня на доске-MMXIV.(2014) Правильно, это год в котором мы сейчас живем. Удобна ли Римская система?(нет) Римская нумерация сравнительно неудобна: записи чисел длинные, письменные вычисления производить невозможно. Римские цифры используют в настоящие время довольно редко.
Отгадайте загадку.
Скачет мячик по страницам.
Ищет он свою сестрицу,
Что имеет вид кольца -
Без начала и конца.(ноль)
Один из величайших древнегреческих математиков Архимед научился называть громадные числа, но обозначать их он не умел.
Ноль это одно из величайших изобретений в математике. Только после того, как люди научились обозначать пропущенные разряды в записи чисел, они получили в руки могучие познания природы. Без нуля не было бы всей современной математики, не было бы и таких достижений человеческого разума, как компьютеров и космических кораблей и много другого. Впервые нуль был придуман вавилонянами примерно две тысячи лет тому назад. Но они применяли его лишь для обозначения пропущенных разрядов в середине числа.
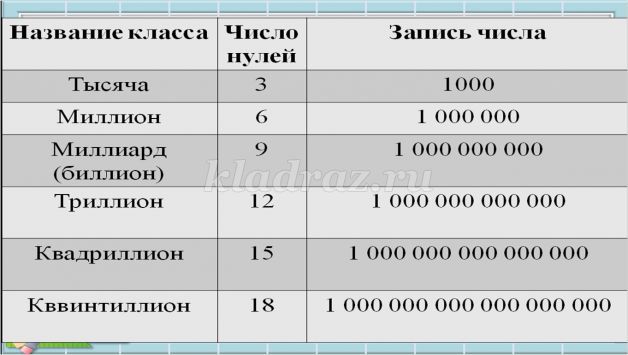
Писать нули в конце записи числа они не догадались. В Индии примерно полторы тысячи лет тому назад нуль был присоединён к девяти цифрам и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно не было. И самое главное, запись таких гигантских чисел стала довольно короткой. Посмотрите на слайд и давайте прочитаем большие числа, которые есть в современном мире. 3-4.
Индийской системой обозначений мы пользуемся до сих пор. В течение многих столетий, переходя от народа к народу, они много раз изменялись, пока приняли современную форму. Арабы заимствовали у индийцев цифры. Европейцы в свою очередь узнали её от арабов. Поэтому наши цифры, в отличие от римских, стали называться арабскими. Правильнее было бы называть их индийскими. Они употребляются в нашей стране начиная примерно с XVII(вывешиваются на доске) века.
Физминутка.
Ноль является натуральным числом? (нет) Ребята назовите мне натуральные числа ? (1,2,3,4….)Мы сейчас ответим с вами на вопрос: Существует ли самое большое натуральное число?
Долгое время люди давали положительный ответ на этот вопрос. Вначале самым большим числом было 2 , затем 3,4…. В древней Руси о числе 10 000 говорили «тьма».
Греции считалось, что самым большим числом является числом песчинок на земле.
Но со временем людям пришлось полностью отказаться от мысли о самом большом числе. Еще Архимед доказал, что счет продолжать неограниченно. Однако потребовалось многие века для того, чтобы идея бесконечности натурального ряда стала общедоступной. Что же таится за многоточием в записи? (что натуральный ряд бесконечен)Правильно, сколько бы не писали, конца и края данной записи нет. Эта запись может продолжаться бесконечно. Всеми этими великими открытиями прошлого мы пользуемся каждый день. Благодаря записи арабскими цифрами мы можем , например умножать в столбик. Давайте мы сейчас с вами посчитаем.
5. Основной этап. Закрепление изученных ранее тем.
Посмотрите на слайд. Отступите от минутки чистописания 2 клетки вниз. Запишите данные примеры в столбик у себе в тетради и решите их. Что вы должны помнить при решении примеров на умножения с нулем? Правильно, мы должны подписывать второй множитель, под числом отличного от нуля. Выполняем самостоятельно. Кто справился-сигнал. (На проверку берется 4 тетради)
А теперь мы с вами вспомним еще один вид заданий- это решения уравнений. Решаем по вариантам. Самостоятельно. 2 человека у доски за шторкой. Проверка.
6. Итог урока. Рефлексия.
На столе у вас лежат листочки. Запишите ряд натуральных чисел до 10. Какие мы использовали цифры? (арабские)С какого века они используются в нашей стране? (17в.) Запишите, XVII век, римскими цифрами. В каком веке мы живем? Запишите. Какие мы использовали цифры?Что вы сегодня узнали нового? С какими системами счисления мы познакомились?
7.Д.з.Самостоятельная работа №5.

Рекомендуем посмотреть:

Конспект урока по природоведению в 3 классе Дидактические игры на уроке математики в 3 классе коррекционной школы Коррекционно-развивающий урок математики, 3 класс. Таблица умножения числа 4 Конспект урока математики в 3 классе: Нумерация чисел в пределах 1000

Похожие статьи:

Математический брейн-ринг, 3 класс. Сценарий

Математический КВН, 3 класс. Сценарий

Внеклассное мероприятие по математике, 3 класс

Внеклассное мероприятие по математике, 4 класс

Внеурочное мероприятие по математике, 3 класс