Мастер-класс по использованию программы Advanced Grapher при графическом решении неравенств с двумя переменными, если функция задана явно.

Назначение: Предлагаю вашему вниманию мастер-класс по использованию программы Advanced Grapher при графическом решении неравенств с двумя переменными, если функция задана явно. Данный материал будет полезен учителям математики, студентам педагогических учебных заведений, учащимся школ 9-11 классов.
Цель: создание наглядного материала при подготовке к уроку
Задача:
- знакомство с возможностями программы Advanced Grapher
- научиться применять программу при решении неравенств, заданных явно

Любому учителю известно, что уроки, посвященные изучению графиков функций, требуют построения большого количества графиков. Чем больше будет построено графиков, тем лучше учащиеся освоят данный материал. Но возникает проблема – ограниченное время урока. Перед учителем встает вопрос о выборе средств и методов обучения с целью обеспечения максимальной эффективности изучения математики. В этом случае приходят на помощь компьютерные технологии. В настоящее время существует много программ, с помощью которых можно рисовать графики функций. Они дают возможность проиллюстрировать свойства функций быстро и наглядно, что повышает и активизирует познавательную деятельность учащихся. На представленном мастер классе используется программа Advanced Grapher
Ход мастер-класса
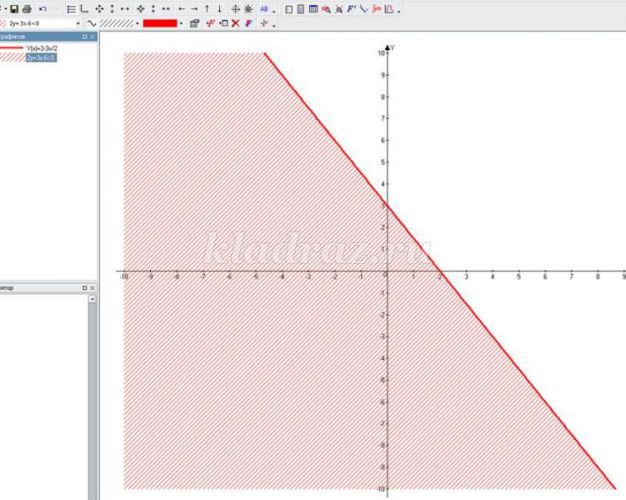
Рассмотрим, как с помощью программы Advanced Grapher изобразить множество решений неравенства Для начала запомним, что все записи в программе выполняются на английском языке.
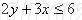
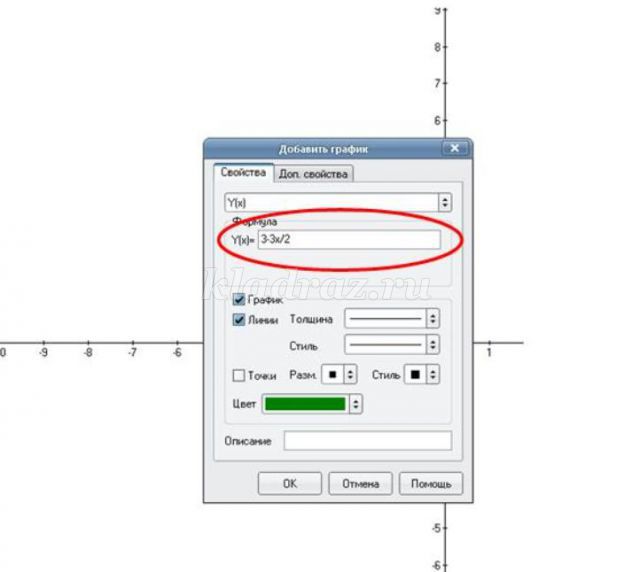
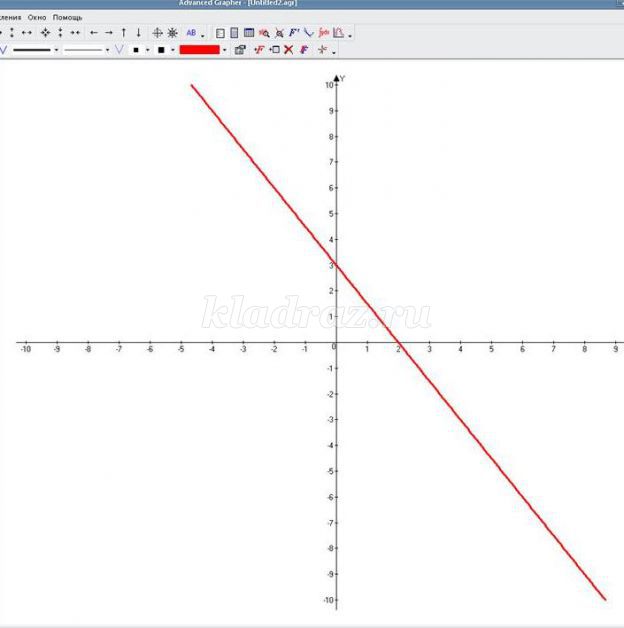
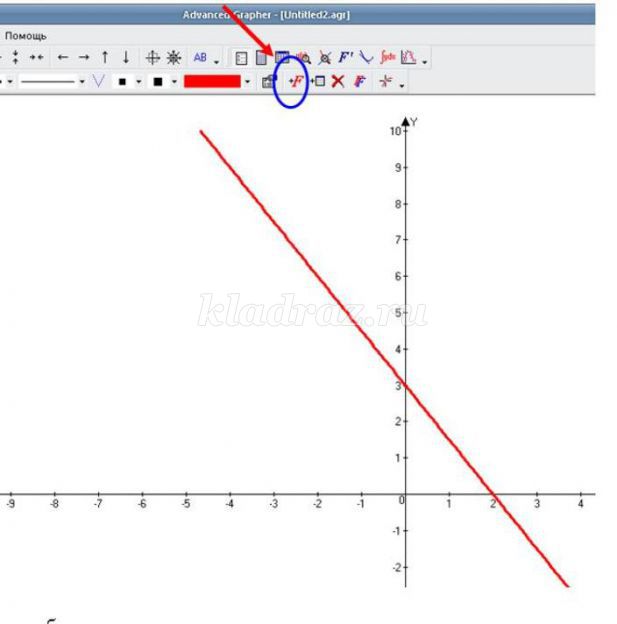
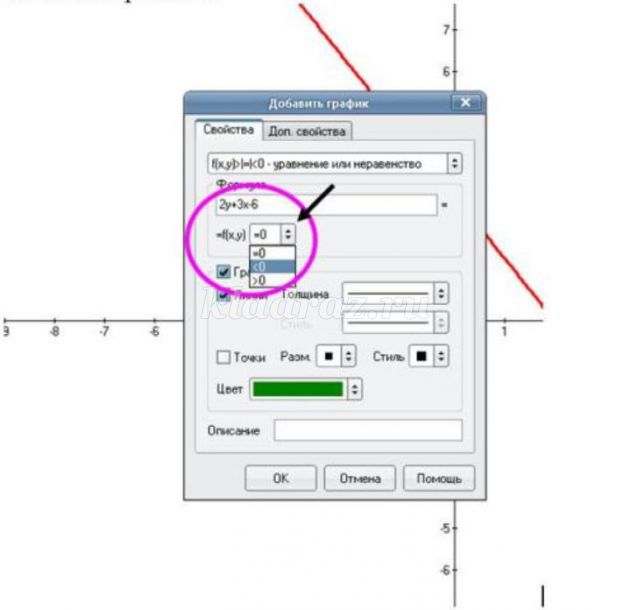
Построим границу неравенства, для этого знак неравенства заменим на знак равно. Функция записано неявно, нам необходимо выразить у через х. Итак, мы нашли, что Подготовительная работа выполнена.
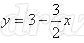
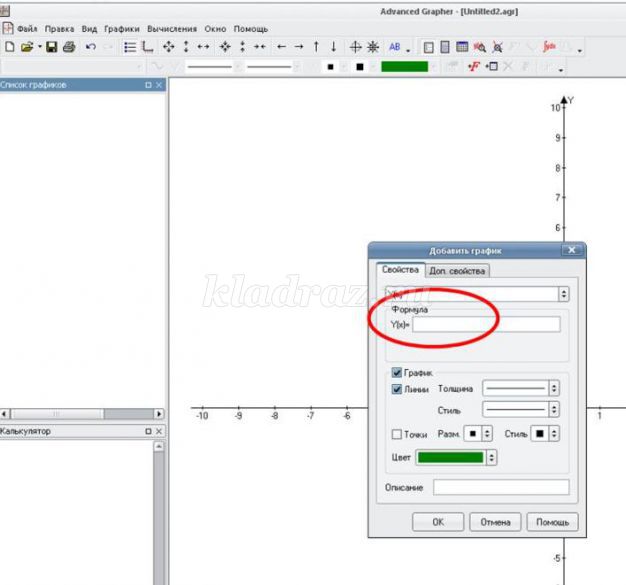
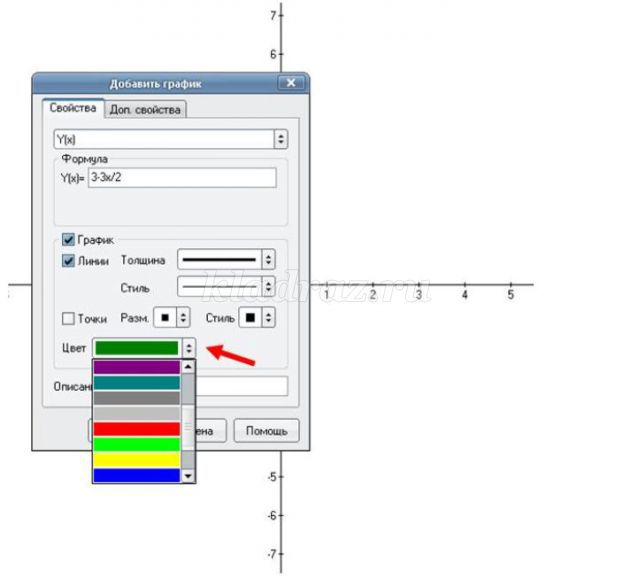
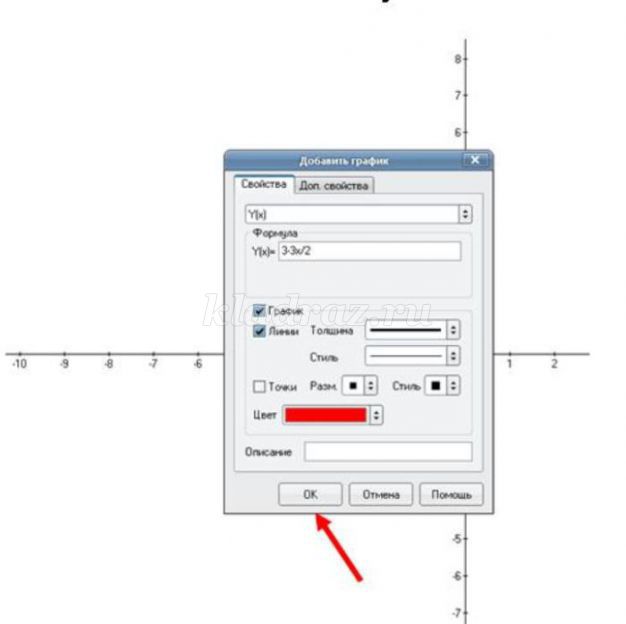
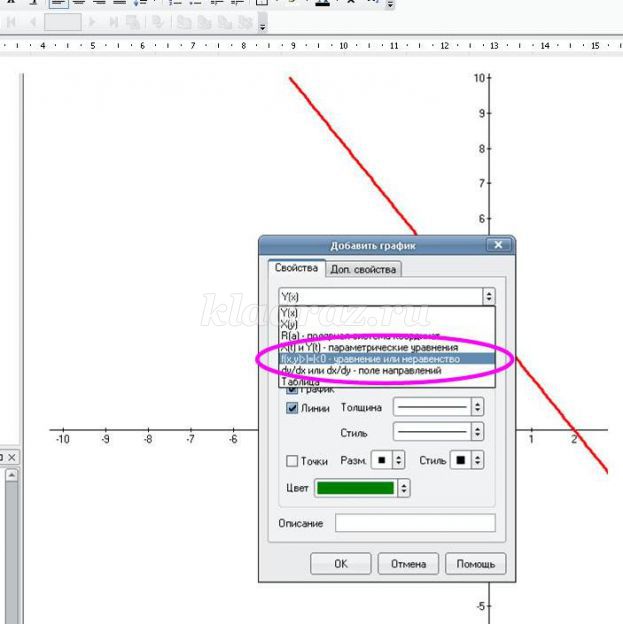
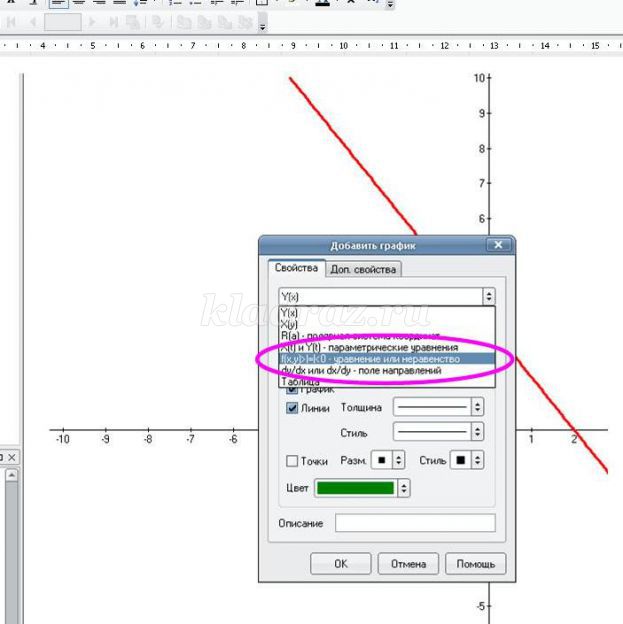
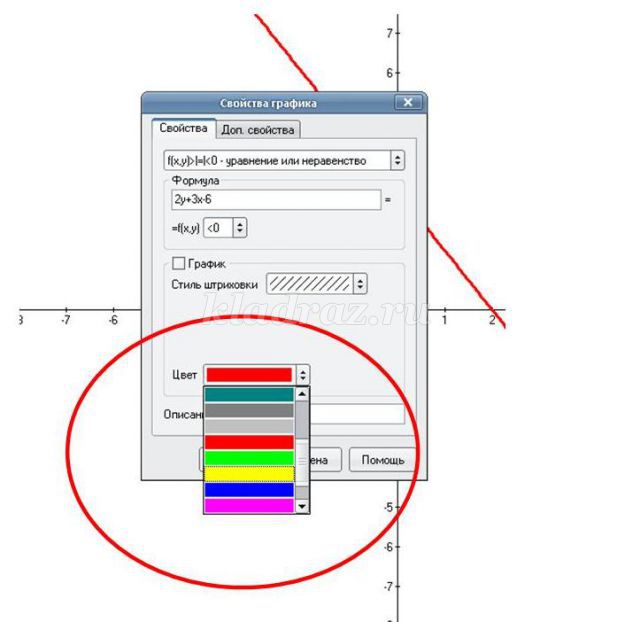
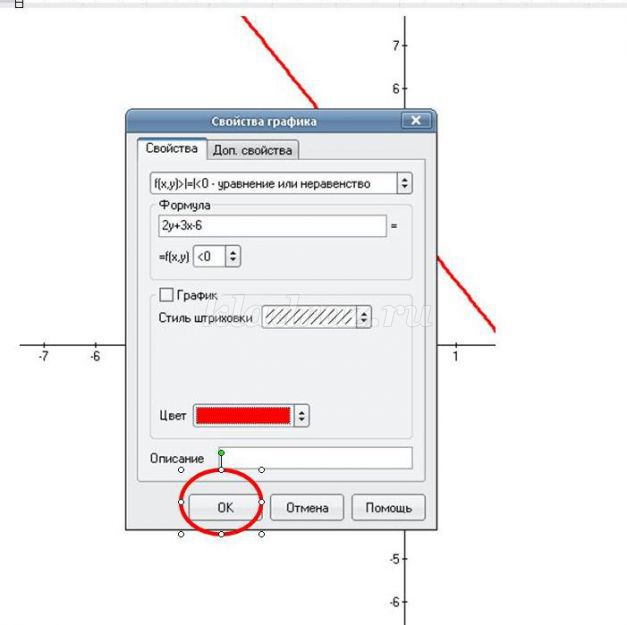
1. Открываем программу Advanced Grapher
2. Нам необходимо построить границу неравенства, для этого нажимаем на кнопку
3. Появится диалоговое окно
4. Нам необходимо записать формулу, мы в отмеченном прямоугольнике вводим 3-3х/2. Помним, что вводим все на английском языке и по правилу записи в данной программе.
5. Выбираем толщину линии, для этого нажимаем на стрелочки и в всплывающем окне выбираем необходимую толщину
6. Далее необходимо выбрать стиль: если знак неравенства нестрогий (больше или равно, меньше или равно, то линия сплошная (если знак неравенства строгий то есть < или >, то разрывная). Нажав на стрелочки, в окне выбираем необходимый стиль линии, в нашем случае – сплошная.
7. Если Вас не устраивает предложенный цвет линии, её также можно поменять. Нажимаем на стрелочки и в появившемся окне с помощью ползунка выбираем необходимый цвет.
8. Больше менять ничего не нужно
9. Далее нажимаем ОК и в результате получаем изображение границы неравенства.
10. Помним, что мы решаем неравенство. Осталось изобразить множество решений данного неравенства. Для этого нажимаем на кнопку
11. В знакомом нам уже окошке выбираем – уравнение или неравенство
12. Необходимо ввести функцию, помним, что вводим функцию на английском языке.
13. Нам дано неравенство а мы вводим 2у+3х-6 и выбираем знак неравенства <, нажав на стрелочки.
14. Далее выбираем такой же цвет, как и у границы неравенства.
15. Нажимаем на ОК
16. Итак, получили графическое решение неравенства
Желаю успехов! Экспериментируйте и все получится.

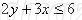
Рекомендуем посмотреть:

Конспект урока математики в 5 классе Математическая игра для 5-6 классов «Скрат на уроке математики» Конспект урока математики в 5 классе. Десятичные дроби Каким должно быть домашнее задание по математике

Похожие статьи:

Математические задачи в сказках с ответами, 5 класс