Конспект урока по алгебре для учащихся 9 класса. Графическое решение неравенств с двумя переменными

Автор: Бондаренко Марина Эдуардовна, учитель ДОШ І-ІІІ ступеней №101 города Донецка Донецкой области
Описание материала: конспект урока по алгебре для учащихся 9 класса по теме «Графическое решение неравенств с двумя переменными (функция задана явно)». Урок ориентирован на учебник «Алгебра, 9 класс» под редакцией С.А.Теляковского, Москва, 2016 Урок с применением программы Advanced Grapher(ранее мы научились работать с данной программой) и метода «Шесть шляп» дает возможность провести урок оживленно, выполнить большой объем работы. Во время урока используется также метод “Ты – мне, я – тебе”, цель - выявить ребят невнимательно слушающих учителя. Суть метода в том, что учитель первым задает вопрос, ждет, кто знает ответ – поднимает зеленый круг, кто сомневается красный. Кто ответил – может задать свой вопрос, ответить может любой желающий.Цель:
Деятельностная цель: Формирование новых знаний и ценностного отношения к ним
Образовательная цель: расширение понятийной базы за счет включения в нее новых элементов.
Задача урока: сформировать навыки графического решения неравенства с двумя переменными
Образовательные задачи урока (формирование познавательных УУД):
- ввести понятие неравенства с двумя переменными.
- составить алгоритм графического решения неравенства.
- сформировать способность применения выведенного алгоритма;
- организовать деятельность учащихся по приобретению необходимых умений и навыков;
- повторить и закрепить умение построения графика уравнения с двумя переменными
Воспитательные задачи урока (формирование коммуникативных и личностных УУД):
- прививать учащимся навыки организации самостоятельной работы;
- формировать умение слушать и вступать в диалог
Развивающие задачи урока: (формирование регулятивных УУД)
- развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей;
- развивать умения слушать и исправлять речь своих товарищей.
Оборудование и наглядность: интерактивная доска, программа Advanced Grapher
Тип урока: изучение нового материала
Ход урока
1. Организационный момент.
Вступительное слово учителя.
2. Сообщение темы и цели урока
На предыдущих уроках мы решали системы уравнений графическим способом, системы уравнений аналитическим способом. Сегодня мы переходим к изучению новой темы «Графическое решение неравенства с двумя переменными». Какая цель нашего урока?
После ответов учащихся учитель подытоживает информацию и предлагает учащимся на «Дереве ожидания» повесить желтый или красный листочек. ( красный – я не справлюсь, тема сложная, желтый – постараюсь разобраться.
Надеваем белую шляпу – и собираем информацию, которая у нас имеется. (учащиеся отвечают).
- Так как мы должны научиться решать неравенства графически, то нам необходимо вспомнить, как строить графики функций.
( С помощью программы Advanced Grapher повторяем, что является графиком элементарных функций, на экран выводятся поочередно графики функций, ученики выбирают соответствующую формулу)


Учитель. Продолжаем анализировать.
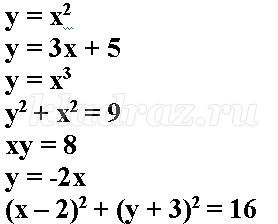
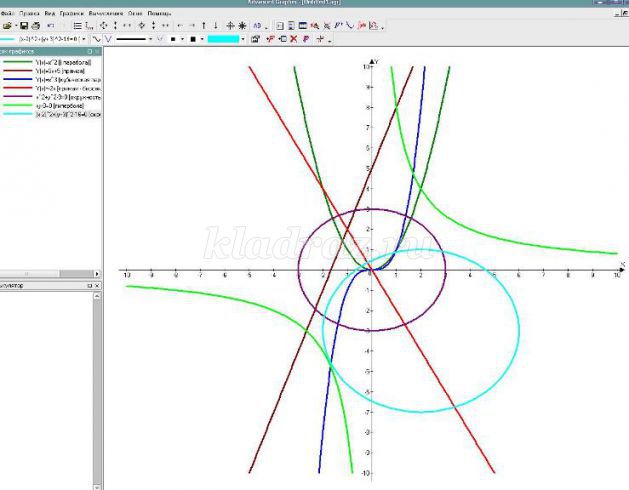
- В теме урока написано слово «неравенство», а мы знаем, что есть числовые неравенства и неравенства с одной переменной.
Учитель: Что такое числовое неравенство? . . . Молодцы! Итак, что еще вы заметили?
- Нам известно, что числовые неравенства могут быть верными и неверными. Неравенства с одной переменной могут быть строгими и нестрогими, линейными и второй степени. Решением неравенства с одной переменной является множество переменной, при которых неравенство обращается в верное числовое неравенство.
Учитель Надеваем черную шляпу – в чем проблема? Что мы не знаем?
У нас неравенство с двумя переменными и мы не знаем, что является решением данного неравенства.
3.Изучение нового материала
Надеваем красную шляпу – ребята выскажите свои предположения по данному вопросу, есть ли у вас предложения, как решить данную проблему.
Так как неравенство с двумя переменными, то решением неравенства является пара значений этих переменных, которая обращает данное неравенство в верное числовое неравенство.
Надеваем желтую шляпу – мы выяснили, что является решением неравенства с двумя переменными. Давайте найдем решения неравенства
Надеваем зеленую шляпу: Пара значений (-1;1) обращает это неравенство в верное числовое неравенство

И является решением неравенства.
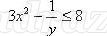
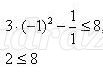
Пара значений (2;1) приводит к неверному числовому неравенству

И не является решением данного неравенства.
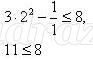
Надеваем синюю шляпу – мы знаем, как изобразить множество решений неравенств с двумя переменными на координатной плоскости?
Схема графического решения неравенства с двумя переменными:
- построить график соответствующего уравнения с двумя переменными.
- выбрать на координатной плоскости точки, обращающие неравенство с двумя переменными в верное числовое неравенство.
Учитель: Итак, нам необходимо изобразить на координатной плоскости множество решений неравенства
Надеваем белую шляпу - нам дано неравенство с двумя переменными. Необходимо изобразить на координатной плоскости множество решений. Как это сделать?
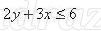
Надеваем черную шляпу – мы не знаем, как решить данное неравенство.
Надеваем красную шляпу – но мы умеем строить график соответствующего уравнения


Надеваем желтую шляпу – мы выяснили, что графиком границы данного неравенства является график уравнения. Она разбивает множество всех точек координатной плоскости на точки, расположенные выше её, и точки, расположенные ниже ее.
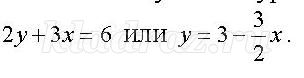
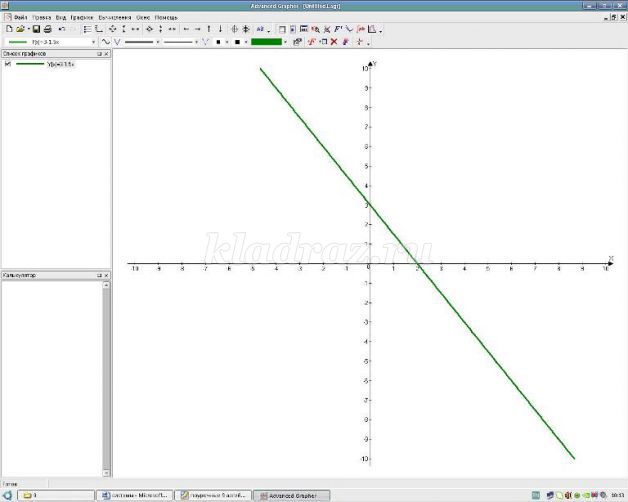
Надеваем зеленую шляпу – возьмем из каждой области по контрольной точке, например, А(0;0) и В(1;5)
Координаты точки А удовлетворяют данному неравенству

Координаты точки В не удовлетворяют данному неравенству

Надеваем синюю шляпу - итак, необходимо выбрать ту область, где находится точка А.

Правило:
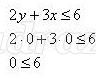
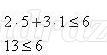
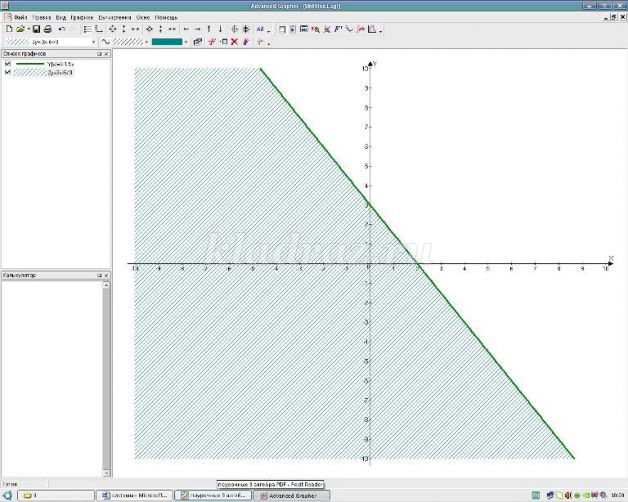
Для того чтобы решить графически неравенство с двумя переменными необходимо:
- построить график соответствующего уравнения, при этом помня, что если неравенство нестрогое то граница входит, если строгое – то не входит.
- изобразить множество решений неравенства
4. Первичное осмысление и закрепление изученного материала.
Как решить неравенства?

Графики каких функций представляет граница данных неравенств? (Выслушиваются ответы учащихся.) Как можно найти решение неравенств?(метод “Ты – мне, я – тебе», цель - выявить ребят невнимательно слушающих учителя.)
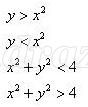
Ученики самостоятельно предлагают алгоритм решения неравенств:
Если неравенство представлено в виде у >f(x), то это неравенство задает на плоскости область, которая лежит не ниже графика.
Если неравенство представлено в виде у<f(x),то это неравенство задает на плоскости область, которая лежит не выше графика.
Решение заданий из учебника
№ 484, 487а,б, 550
Учащиеся решают используя метод «Шесть шляп» и решение выводят на экран.
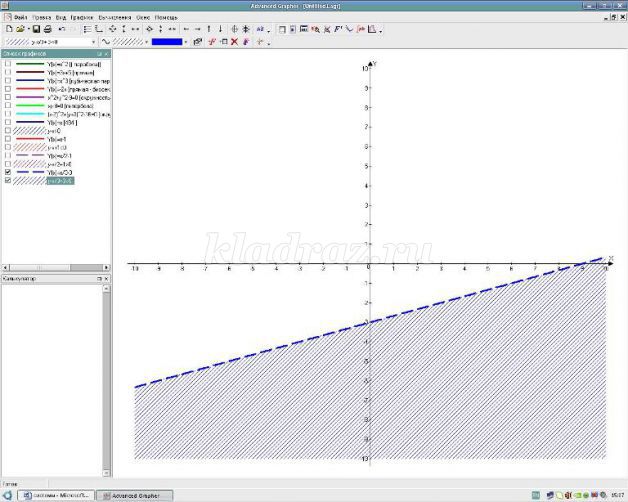
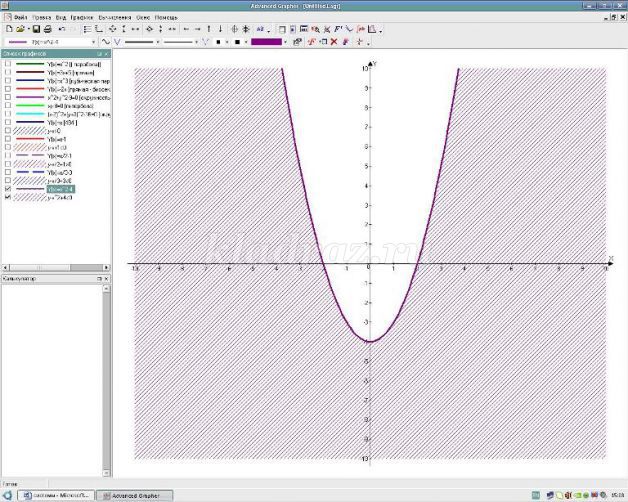
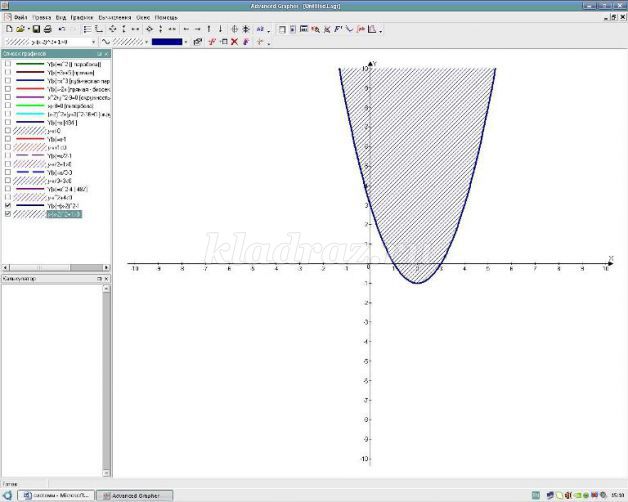
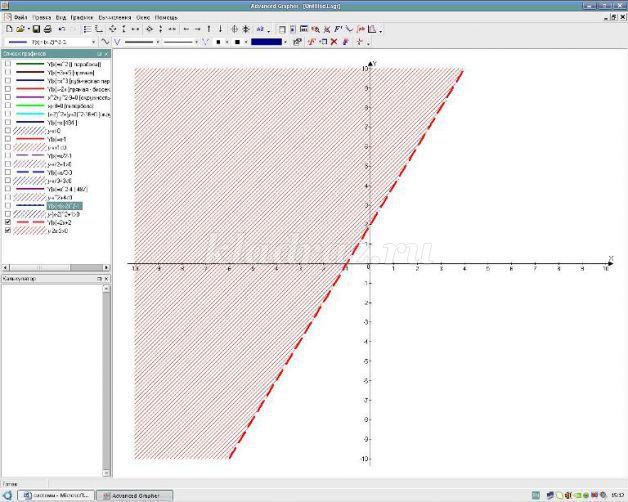
Пример объяснения хода решения неравенства.
Надеваем белую шляпу - нам дано неравенство с двумя переменными. Необходимо изобразить на координатной плоскости множество решений. Как это сделать?
Надеваем черную шляпу – необходимо выяснить что является графиком соответствующего уравнения и какой линией изобразить ( сплошной или нет)
Надеваем красную шляпу – графиком границы является прямая, чтобы ее построить, необходимо знать координаты двух точек. Например, это (0;0) и (2;2). Так как неравенство нестрогое, то линия сплошная.

Надеваем желтую шляпу – мы выяснили, что графиком границы данного неравенства является прямая. Она разбивает множество всех точек координатной плоскости на точки, расположенные выше её, и точки, расположенные ниже ее.
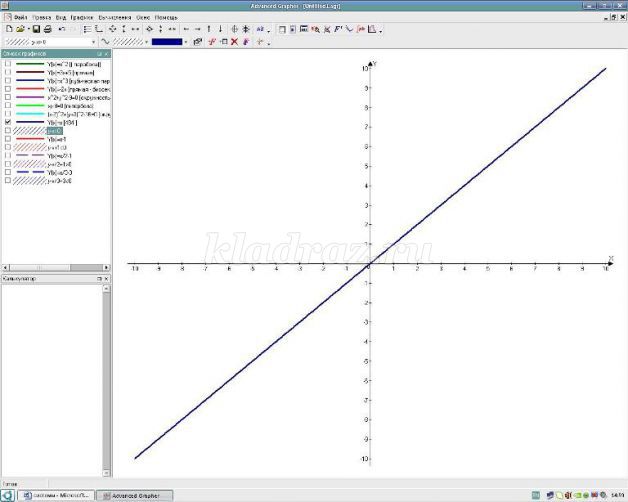
Надеваем зеленую шляпу - так нам необходимо решить неравенство, содержащие знак больше или равно, то выбираем ту часть координатной плоскости, которая лежит выше.
Надеваем синюю шляпу – изображаем решение неравенства

Аналогичные рассуждения предлагают учащиеся



№ 487а,б


№ 550


№ 554а

5. Итог урока
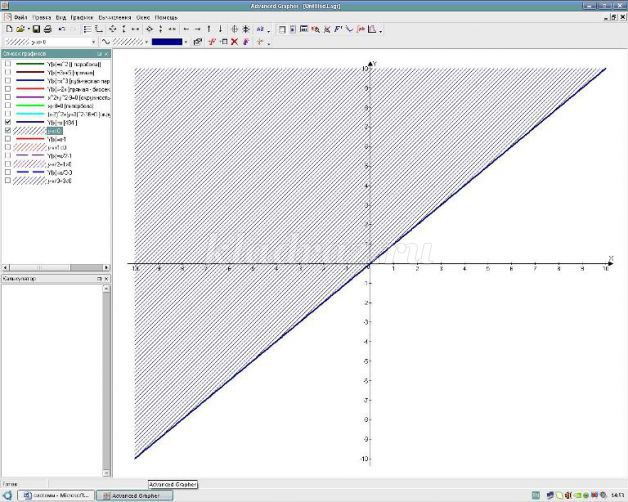
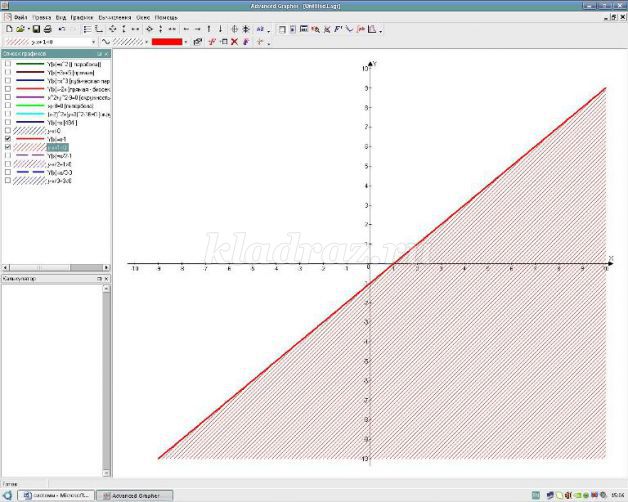
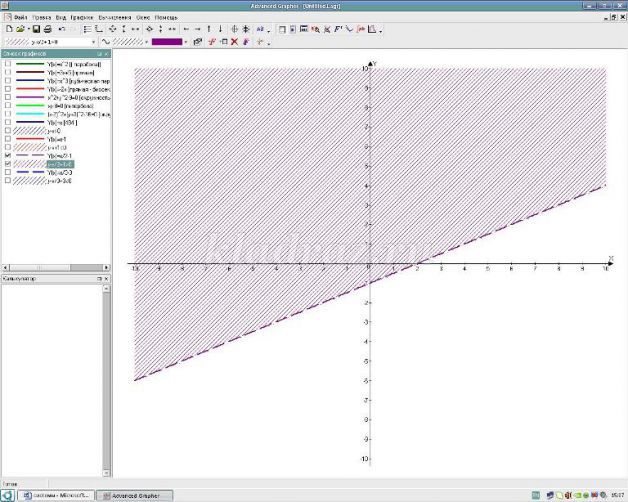
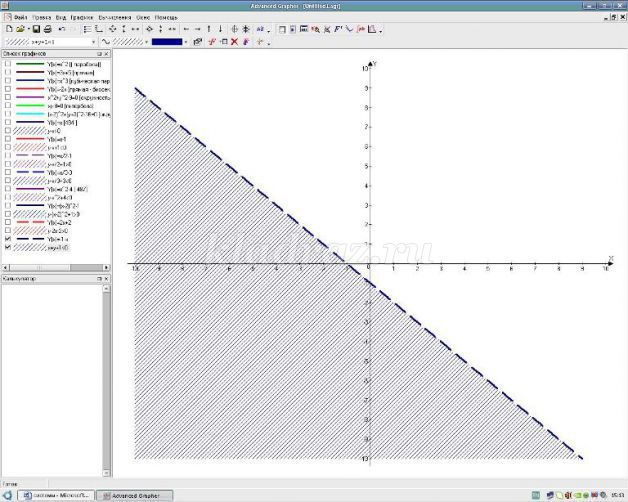
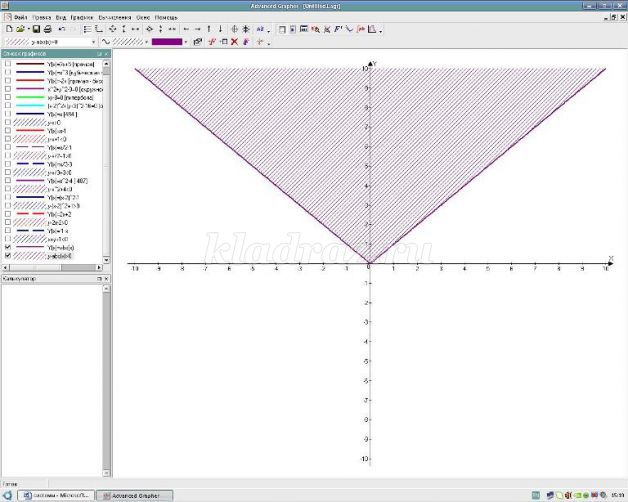
Надеваем синюю шляпу: с какими определениями сегодня познакомились, как графически решить неравенство с двумя переменными, на что необходимо обратить внимание?
После ответов учащихся учитель предлагает учащимся на «Дереве ожидания» повесить желтый или красный листочек. ( красный – я не понял тему, желтый – я научился решать)
Сравниваем дерево в начале урока и в конце, делаем соответствующий вывод (на что необходимо обратить внимание на следующем уроке как учителю, так и ученикам)
6. Домашнее задание.
Выучить п 21., решить №485, 491, 554б

Рекомендуем посмотреть:

Конспект урока математики в 5 классе Математическая игра для 5-6 классов «Скрат на уроке математики» Конспект урока математики в 5 классе. Десятичные дроби Каким должно быть домашнее задание по математике

Похожие статьи:

Математические задачи в сказках с ответами, 5 класс