Конспект урока по алгебре для учащихся 9 класса по теме «Графическое решение неравенств с двумя переменными (функция задана неявно)»
Автор: Бондаренко Марина Эдуардовна, учитель ДОШ І-ІІІ ступеней №101 города Донецка Донецкой области
Описание материала: конспект урока по алгебре для учащихся 9 класса по теме «Графическое решение неравенств с двумя переменными (функция задана неявно)». Урок ориентирован на учебник «Алгебра, 9 класс» под редакцией С.А.Теляковского, Москва, 2016 . Урок с применением программы Advanced Grapher
Деятельностная цель: Формирование новых знаний и ценностного отношения к ним
Образовательная цель: формирование умений решать неравенства в случае неявного задания функции
Задача урока: формирование умения решать графически неравенства с двумя переменными, если функция задана неявно
Образовательные задачи урока (формирование познавательных УУД):
- составить алгоритм графического решения неравенства ( функция задана неявно).
- сформировать способность применения выведенного алгоритма;
- организовать деятельность учащихся по приобретению необходимых умений и навыков;
Воспитательные задачи урока (формирование коммуникативных и личностных УУД):
- прививать учащимся навыки организации самостоятельной работы;
- формировать умение слушать и вступать в диалог
Развивающие задачи урока: (формирование регулятивных УУД)
- развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей;
- развивать умения слушать и исправлять речь своих товарищей;
Оборудование и наглядность: интерактивная доска, программа Advanced Grapher
Тип урока: изучение нового материала
Ход урока
1. Организационный момент.
Вступительное слово учителя.
2. Проверка домашнего задания
№485
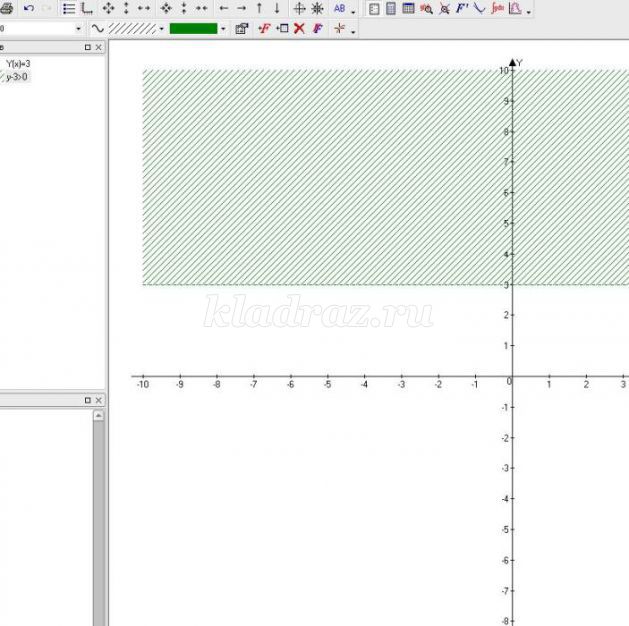
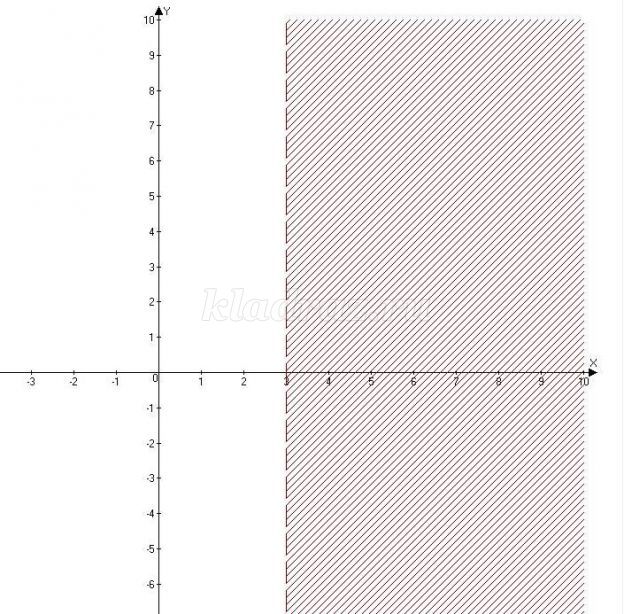 № 554б
№ 554б
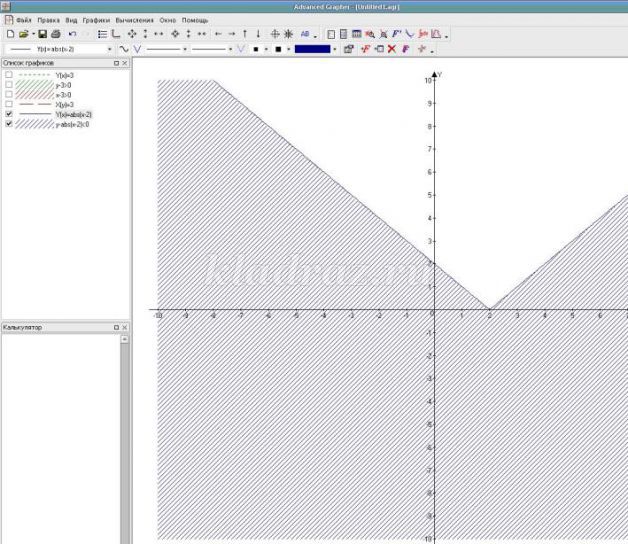 3.Изучение нового материала
3.Изучение нового материала
Часть учащихся на предыдущем занятии получили задание: решить ТОГИС задачу, которую на данном уроке они должны объяснить всем учащимся.
Итак, перед нами была поставлена задача: изобразить множество решений неравенства
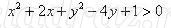 на координатной плоскости.
на координатной плоскости.
Ученик анализирует:
- Какую видим проблему: Функция задана неявно.
- Что мы уже умеем: построим график уравнения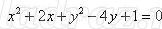 Для этого выделим в уравнении полный квадрат:
Для этого выделим в уравнении полный квадрат:
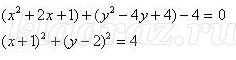 Это уравнение окружности с центром в точке (-1;2) и радиусом 2. Построим эту окружность.
Это уравнение окружности с центром в точке (-1;2) и радиусом 2. Построим эту окружность.
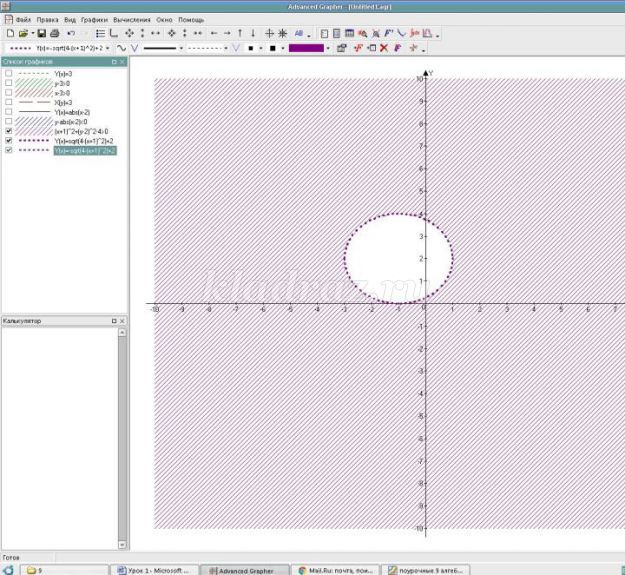
- Что мы заметили: данное неравенство строгое, а значит граница – не сплошная линия.
- Осталось изобразить множество решений данного неравенства. Если подставим координаты центра окружности в неравенство, то получим, что данная точка не удовлетворяет неравенству, а значит, не является решением неравенства. Итак, можно сделать вывод, что неравенству удовлетворяют точки, расположенные вне окружности.
 Нам было предложение также задание изобразить на координатной плоскости множество решений неравенства
Нам было предложение также задание изобразить на координатной плоскости множество решений неравенства 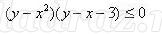 Анализируем:
Анализируем:
- Что мы видим: функция задана неявно
- Что мы умеем: построим график уравнения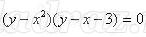 Графиком уравнения является
Графиком уравнения является 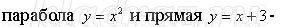 - Что мы заметили: данное неравенство не строгое, а значит граница –сплошная линия.
- Что мы заметили: данное неравенство не строгое, а значит граница –сплошная линия.
- Осталось изобразить множество решений данного неравенства. Я предлагаю Вам это сделать самостоятельно и затем сверить решение.
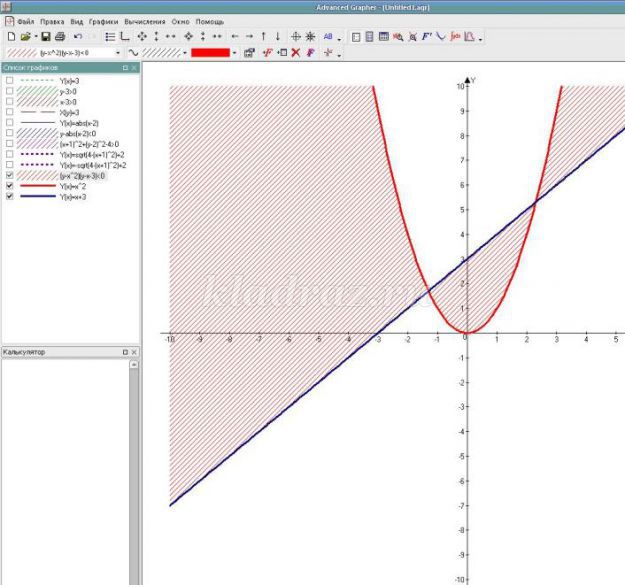 В ходе решения этих заданий наша творческая группа пришла к выводу:
В ходе решения этих заданий наша творческая группа пришла к выводу:
Если f(x;у)=0– замкнутая линия, то неравенство f(x;у)>0, задает область, лежащую вне замкнутой линии, а неравенство f(x;у)<0 – область лежащую внутри.
Учитель предлагает наиболее универсальное, полезное для проверки правило.
“Правило пробной точки”
1. Построить F(x;y) =0
2 .Взяв из каждой области пробную точку, установить, являются ли ее координаты решение неравенства.
3. Показать область решения неравенства.
4. Первичное осмысление изученного материала.
Решение заданий из учебника с объяснением с использованием программы Advanced Grapher
№487 (в,г), №489а, 490б
Активный метод отдыха “Стрельба глазами”.
Перед серьезным заданием необходима небольшая пауза. Ребятам предлагаю отдохнуть, делая зарядку для глаз. Нарисовать глазами геометрические фигуры: квадрат, ромб, прямоугольник, разного рода треугольники, трапецию, параллелограмм. И, наконец, стрельба глазами: вверх, вниз, вправо, влево. Можно предложить посмотреть на цветок, окно, нос, на соседа.
5. Творческие задания
Учащиеся решают самостоятельно с последующей проверкой.
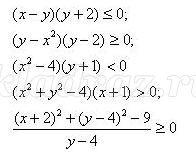 6. Домашнее задание
6. Домашнее задание
Выучить п 22, конспект, решить № 489б, 490а,
 7. Итог урока
7. Итог урока
«Микрофон» Я узнал сегодня на уроке . . ., научился .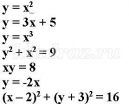 Конспект урока по алгебре для учащихся 9 класса. Графическое решение неравенств с двумя переменными
Конспект урока по алгебре для учащихся 9 класса. Графическое решение неравенств с двумя переменными
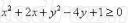 Использование программы Advanced Grapher при графическом решении неравенств с двумя переменными, есл
Использование программы Advanced Grapher при графическом решении неравенств с двумя переменными, есл
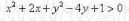 Мастер-класс по использованию программы Advanced Grapher при графическом решении неравенств с двумя
Мастер-класс по использованию программы Advanced Grapher при графическом решении неравенств с двумя
Описание материала: конспект урока по алгебре для учащихся 9 класса по теме «Графическое решение неравенств с двумя переменными (функция задана неявно)». Урок ориентирован на учебник «Алгебра, 9 класс» под редакцией С.А.Теляковского, Москва, 2016 . Урок с применением программы Advanced Grapher
Тема: Графическое решение неравенства с двумя переменными (функция задана неявно)
Цель:Деятельностная цель: Формирование новых знаний и ценностного отношения к ним
Образовательная цель: формирование умений решать неравенства в случае неявного задания функции
Задача урока: формирование умения решать графически неравенства с двумя переменными, если функция задана неявно
Образовательные задачи урока (формирование познавательных УУД):
- составить алгоритм графического решения неравенства ( функция задана неявно).
- сформировать способность применения выведенного алгоритма;
- организовать деятельность учащихся по приобретению необходимых умений и навыков;
Воспитательные задачи урока (формирование коммуникативных и личностных УУД):
- прививать учащимся навыки организации самостоятельной работы;
- формировать умение слушать и вступать в диалог
Развивающие задачи урока: (формирование регулятивных УУД)
- развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей;
- развивать умения слушать и исправлять речь своих товарищей;
Оборудование и наглядность: интерактивная доска, программа Advanced Grapher
Тип урока: изучение нового материала
Ход урока
1. Организационный момент.
Вступительное слово учителя.
2. Проверка домашнего задания
№485



Часть учащихся на предыдущем занятии получили задание: решить ТОГИС задачу, которую на данном уроке они должны объяснить всем учащимся.
Итак, перед нами была поставлена задача: изобразить множество решений неравенства
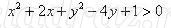
Ученик анализирует:
- Какую видим проблему: Функция задана неявно.
- Что мы уже умеем: построим график уравнения
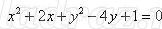
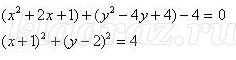
- Что мы заметили: данное неравенство строгое, а значит граница – не сплошная линия.
- Осталось изобразить множество решений данного неравенства. Если подставим координаты центра окружности в неравенство, то получим, что данная точка не удовлетворяет неравенству, а значит, не является решением неравенства. Итак, можно сделать вывод, что неравенству удовлетворяют точки, расположенные вне окружности.

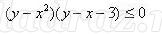
- Что мы видим: функция задана неявно
- Что мы умеем: построим график уравнения
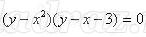
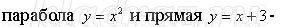
- Осталось изобразить множество решений данного неравенства. Я предлагаю Вам это сделать самостоятельно и затем сверить решение.

Если f(x;у)=0– замкнутая линия, то неравенство f(x;у)>0, задает область, лежащую вне замкнутой линии, а неравенство f(x;у)<0 – область лежащую внутри.
Учитель предлагает наиболее универсальное, полезное для проверки правило.
“Правило пробной точки”
1. Построить F(x;y) =0
2 .Взяв из каждой области пробную точку, установить, являются ли ее координаты решение неравенства.
3. Показать область решения неравенства.
4. Первичное осмысление изученного материала.
Решение заданий из учебника с объяснением с использованием программы Advanced Grapher
№487 (в,г), №489а, 490б
Активный метод отдыха “Стрельба глазами”.
Перед серьезным заданием необходима небольшая пауза. Ребятам предлагаю отдохнуть, делая зарядку для глаз. Нарисовать глазами геометрические фигуры: квадрат, ромб, прямоугольник, разного рода треугольники, трапецию, параллелограмм. И, наконец, стрельба глазами: вверх, вниз, вправо, влево. Можно предложить посмотреть на цветок, окно, нос, на соседа.
5. Творческие задания
Учащиеся решают самостоятельно с последующей проверкой.
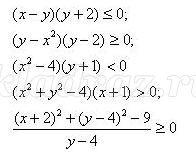
Выучить п 22, конспект, решить № 489б, 490а,

«Микрофон» Я узнал сегодня на уроке . . ., научился .
Рекомендуем посмотреть:
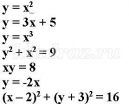 Конспект урока по алгебре для учащихся 9 класса. Графическое решение неравенств с двумя переменными
Конспект урока по алгебре для учащихся 9 класса. Графическое решение неравенств с двумя переменными
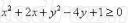 Использование программы Advanced Grapher при графическом решении неравенств с двумя переменными, есл
Использование программы Advanced Grapher при графическом решении неравенств с двумя переменными, есл
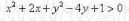 Мастер-класс по использованию программы Advanced Grapher при графическом решении неравенств с двумя
Мастер-класс по использованию программы Advanced Grapher при графическом решении неравенств с двумя
Участник №138 профессионального конкурса педагогического мастерства с 15 января по 15 апреля 2016 года
← Конспект урока по алгебре для учащихся 9 класса. Графическое решение неравенств с двумя переменными | Использование программы Advanced Grapher при графическом решении неравенств с двумя переменными, если функция задана неявно →
|
|
Автор: Марина Эдуардовна Бондаренко
Опубликовано: 3285 дней назад (27 марта 2016)
Просмотров: 2541
Рубрика: Конспекты уроков
|
+1↑ Голосов: 3 |
Нет комментариев. Ваш будет первым!



