Занимательные задачи для младших школьников
(Нестандартные задачи на деление)
Задача 1. Трехметровый брусок надо разрезать на полуметровые. Сколько разрезов надо сделать?
Решение: в трехметровом бруске 300 см. Его надо разрезать на бруски длиной 50 см каждый. Получится: 300 : 50 = 6 (брусков). А сколько же надо сделать разрезов? Рассуждать будем так: чтобы разделить брусок пополам, то есть на 2 части, надо сделать один разрез, на три части - два разреза, и так далее, на шесть частей - пять разрезов. Итак, надо сделать 6-1=5 (разрезов).
Ответ: 5 разрезов.
При решении подобных задач возможны различные варианты. Рассмотрим их на следующих примерах.
Задача 2. Пятидесятиметровый шнур надо разрезать на части, длина каждой из которых 2 м. Сколько разрезов надо сделать?
Решение: 50 : 2 - 1 = 24 (разреза).
Ответ: 24 разреза.
Задача 3. Шестиметровый брус разрезали на равные части, сделав при этом 5 разрезов. Какой длины получились каждая часть?
Решение: 6 : (5 + 1) = 1 (м).
Ответ: 1 метр.
Задача 4. Вдоль участка длиной 100 м поставили столбы для ограды на расстоянии друг от друга -4 м. Сколько столбов поставили?
Решение: 100 : 4 + 1 = 25 + 1 = 26 (столбов).
Ответ: 26 столбов.
Задача 5. Вдоль прямой дороги на расстоянии 150 м поставили 51 столб. Столбы ставились на равном расстоянии друг от Друга. Каково это расстояние?
Решение: 150 : (51 - 1) = 3 (м).
Ответ: на расстоянии 3 метра друг от друга.
Задачи-ребусы.
1. Найдите цифры, обозначенные буквами А и В в примере:
Решение основано на том, что переноса единиц из одного разряда в другой нет. Значит А + В = 3.
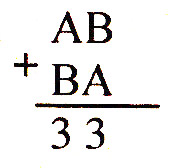
Поскольку число не может начинаться с 3 3 нуля, то возможны случаи: А = 1, В = 2 или А = 2, В = 1, то есть
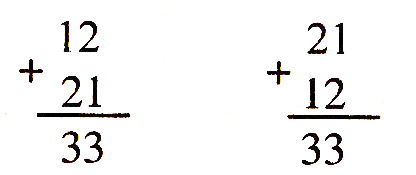
Ответ: А = 1, В = 2 или А = 2, В = 1.
Учитель, однако, может пояснить учащимся, что А = 2, В = 1 не дает принципиально нового решения. Это обстоятельство очень важно, поскольку в элементарной форме подготавливает учащихся к восприятию такого свойства, как симметричность.
После этого учащимся могут быть предложены такие задачи:
Задача 1. Найдите цифры, обозначенные буквами А, В, С в примере:

Задача 2. Какие цифры надо поставить вместо звездочек в примере?
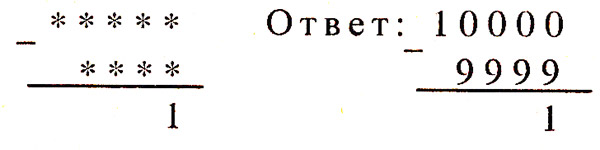
Задача 3. Какие цифры надо поставить в примере вместо звездочек?
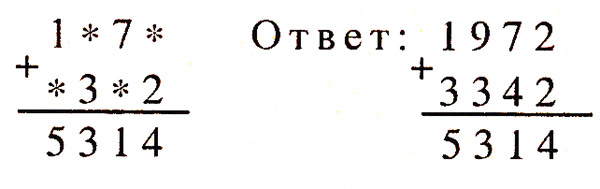
Задача 4. Какие цифры скрываются за звездочками?
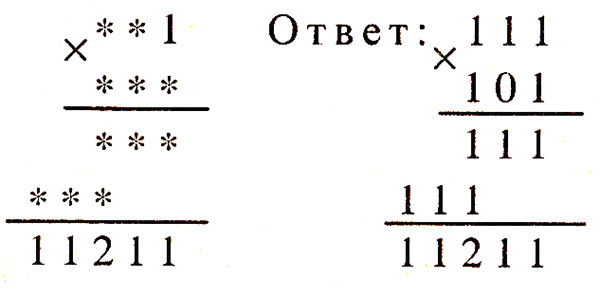
Задачи-эксперименты.
Задача 1. Предложите учащимся взять произвольно три различные цифры, кроме нуля, а затем составить из них всевозможные трехзначные числа, сложить их и полученную сумму разделить на сумму первоначально взятых цифр. Учащимся можно сразу сообщить ответ - 222.
Например, учащиеся взяли цифры 2, 3, 7. Они составили из них шесть трехзначных чисел: 237, 273, 327, 372, 723, 732. Сумма их равна: 237 + 273 + 327 + 372 + 723 + 732 = (237 + 723) + (273 + + 327) + (372 + 732) = 960 + 600+1104 = 2664.
Разделив это число на сумму цифр 7 + 3 + 2, учащиеся получают ответ: 2664 : 12 = 222.
Эта задача очень интересна. Удивление вызывает угадывание ответа учителем. Особенно удивительно то, что учитель угадал ответ у каждого из учеников. Несмотря на то, что цифры были взяты ими совершенно произвольно и в весьма разнообразных сочетаниях. Но это эмоциональная сторона дела, хотя ее роль в обучении математике младших школьников представляется весьма важной. В задаче немало и поучительных математических моментов.
Во-первых, обратим внимание учащихся на то, что из трех цифр можно составить именно шесть чисел. Это несложно, на первое место можно поставить любую из трех цифр, а на оставшиеся - две другие в разном порядке. Значит, всего таких чисел 3x2 = 6.
Во-вторых, при сложении чисел чрезвычайно полезными оказываются навыки рационального выполнения действий, что приводит к результату значительно быстрее, и уменьшает возможность допущения ошибок.
В-третьих, и это главное, весьма интересно решение задачи в общем виде. Итак, пусть взяты цифры a, b, с (различные, ни одна из цифр не равна нулю). Составим из них шесть трехзначных чисел. Каждая цифра, например, а, будет дважды означать число сотен, дважды - десятков, дважды - единиц. Значит, сумма всех шести чисел будет равна.
100 (2а + 2b + 2с) + 10 (2а + 2b + 2с) + (2а + 2b + 2с) = 222 (а + b + с), и результат от деления этой суммы на сумму цифр (а + b + с) будет равен 222.
Учащимся будут интересны и другие задачи такого типа.
Задача 2. Возьмите любое трехзначное число, не оканчивающееся нулем. Переставьте в нем цифры в обратном порядке. ц3 большего числа вычтите меньшее и полученную разность разделите на разность первых цифр слева этих двух чисел. У вас получится 99. Почему?
Например, взяли число 285, переставили в нем цифры, получили 582. Из большего вычли меньшее 582 - 285 = 297 и разделили на разность первых цифр 5-2 = 3, получили 297 : 3 = 99.
Задача 3. Задумайте число, которое делилось бы на 6. Разделите его пополам, полученное число запомните. Теперь задуманное число разделите на 3, результат запомните. А теперь разделите задуманное число на 2. Результаты всех трех делений сложите. У вас получилось задуманное число. Почему?
Например, взяли число 72, получили три числа:
первое - 72 : 2 = 36,
второе - 72 : 3 = 24,
третье - 72 : 6 = 12.
Сложили их: 36 + 24 + 12 = 72. Получили задуманное число.
Задача 4. Возьмите любое двузначное число, которое не оканчивается нулем. Переставьте в нем цифры, получите новое число. Сложите эти два числа и разделите их на сумму цифр любого из этих чисел. Докажите, что в ответе получается 11.
Например, взяли число 53. Переставили в нем цифры, получили число 35. Сложили их и получили 35 + 53 = 88.
Сумму разделили на сумму цифр первого числа 5 + 3 = 8 (у второго она та же), получили 88 : 8 = 11.
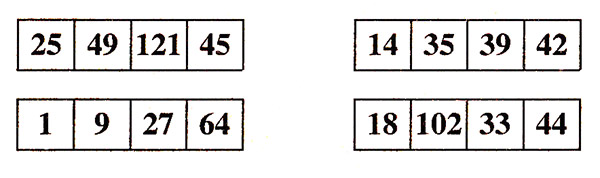
Задача «Четвертый лишний».
В каждом ряду три числа обладают общим свойством, а одно число этим свойством не обладает. Укажите, что это за свойство и какое число лишнее.
Похожие статьи:
Внеурочное мероприятие по математике, 1 класс
Задачи в стихах для устного счета, 3 класс
Математические загадки для 1 класса с ответами в стихах
Занимательное занятие по математике, 2-3 класс
Математические сказки для начальной школы