Опыт работы учителя математики. Особенности преподавания математики для разных групп старшей школы

Добрый день, уважаемые коллеги.
Я работаю учителем математики Усть-Качкинской средней школы.
В этом учебном году я впервые преподаю профильную математику. У нас в старшей школе образовательный процесс организован таким образом, что позволяет обучающимся реализовывать собственную индивидуальную образовательную траекторию.

В начале 10 класса на основе выбора обучающихся были сформированы группы согласно выбранным профилям: физико-математическая, химико-биологическая, социально-экономическая и гуманитарная. Профильная математика востребована для учащихся физико-математической и социально-экономической групп.

Общая численность детей 10 класса, изучающих математику на профильном уровне 13 человек: 6 человек, сопутствующий профильный предмет физика и перспектива получения инженерных профессий и 7 человек – социально-экономической направленности – сопутствующие профильные предметы – право, экономика, обществознание. Уроки математики для этих детей совместные.

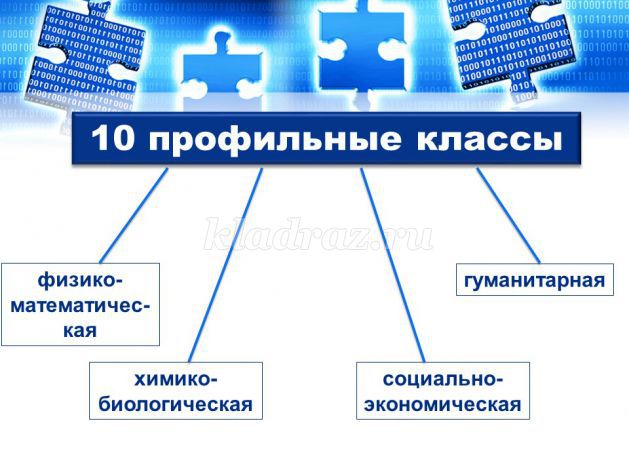
Программа профильного уровня с точки зрения содержания должна быть качественно реализована для всех обучающихся. И уровень достижения результата должен обеспечивать гарантированное поступление в высшие учебные заведения.

Математика – это прикладная наука, позволяющая моделировать и исследовать различные объекты, процессы, явления. Я как учитель математики ставлю для себя цель показать учащимся прикладную направленность предмета.

Поэтому для обучающихся физико-математического профиля для отработки содержания внутри тем подбираются задачи и тексты, описывающие физические объекты, явления и процессы. Для обучающихся социально-экономического направления – задания, тексты, содержащие экономические, общественные процессы и явления. Это необходимо для того, чтобы поддерживать мотивацию и профильную направленность выбора ребенка.
В соответствии с этим я выделила темы, по которым подобрала банк заданий для профилей: Производная, применение производной к исследованию функции, теория вероятностей и статистика.

Например, при изучении темы «Исследование функции с помощью производной», я предлагаю задачи следующего содержания:
• Для социально-экономической группы:
• Зависимость покупательной активности жителей города N от времени суток выражается формулой: p = t3 − 6t2 + 6, где t – время, р – покупательная активность. Определите, в какое время суток наблюдается минимум покупательной активности.
Или
• Некоторая компания продаёт свою продукцию по цене p = 600 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v = 300 руб., постоянные расходы предприятия f = 700 000 руб. в месяц. Месячная операционная прибыль предприятия, выраженная в рублях, вычисляется по формуле: π(q) = q(p − v) − f. Определите наименьший месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет максимальной.

Для физико-математической:
• Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 1,6 + 8t − 5t2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. В какой момент времени высота подъема мяча будет максимальной?
• На верфи инженеры проектируют новый подводный зонд для изучения морских глубин. Конструкция будет крепиться ко дну при помощи троса. Зонд имеет кубическую
форму, а значит, сила натяжения троса определяется по формуле: T = ρ gl 3 − mg, где l — линейный размер аппарата в метрах, ρ=1000 кг/м3 — плотность воды, g — ускорение свободного падения, а m = 129 кг — масса зонда. Каковы могут быть максимальные линейные размеры зонда, чтобы обеспечить его эксплуатацию в условиях, когда сила натяжения троса будет наибольшей.

Сейчас я вам представлю примеры задач, которые применяются в теме «Статистика и теория вероятностей»:
Для социально-экономической группы:
• В конкурсе на занятие пяти вакансий участвуют семь претендентов (Результаты тестирования каждого претендента, на соответствующие вакансии, даны в виде таблицы.) Тестирование производилось по десятибалльной шкале. Определить, какого претендента и на какую вакансию следует принять, причем так, чтобы сумма баллов отобранных претендентов оказалось максимальной.
• Фермер может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равна соответственно 0,25, 0,30 и 0,45. Если цены возрастут, урожай кукурузы даст 30 000 чистого дохода, а урожай соевых бобов — 10 000. Если цены останутся неизменными, фермер лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 35 000 и 5 000. соответственно. Постройте дерево решений. Какую культуру следует выращивать фермеру? Каково ожидаемое значение его прибыли?

Для физико-математической:
• Пылинки массой m=10-18 г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1 %. Температура T воздуха во всем объеме одинакова и равна 300 Кельвинов.
• Барометр в кабине летящего самолета все время показывает одинаковое давление p=79 кПа, благодаря чему летчик считает высоту h1 полета неизменной. Однако температура воздуха за бортом самолета изменилась с t1=5 °С до t2=1 °С. Какую ошибку Δh в определении высоты допустил летчик? Давление р0 у поверхности Земли считать нормальным.

Экономические задачи представлены в современных кимах ЕГЭ , 17-ой задачей. И решать данные задачи должны все ученики группы вне зависимости от выбранного профиля.
• Какой вклад выгоднее: первый — на 1 год под 13 % годовых, или второй — на 3 месяца (с автоматической пролонгацией каждые три месяца в течение года) под 12 % годовых? При расчётах считайте, что один месяц равен 1\12 части года.
• По бизнес-плану предполагается вложить в четырёхлетний проект 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 13 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум утроятся.

Конечно, задачи связаны с заявленными профилями только формально, но решение таких задач наиболее полезно и значимо для ребенка, чем просто решать задачу с абстрактными величинами, сразу видно прикладное применение математики и это позволяет сохранить мотивацию учащихся на высоком уровне.

Обогащение школьного курса за счет задач, направленных на конкретный профиль оказывает неоценимую поддержку (услугу) и обучению математике, и изучению профильных предметов.

Тема эта не простая, требует много времени для подготовки, но я буду ее продолжать и применять в работе.

Скачать эту презентацию

Рекомендуем посмотреть:

Конспект урока математики в 5 классе Математическая игра для 5-6 классов «Скрат на уроке математики» Конспект урока математики в 5 классе. Десятичные дроби Каким должно быть домашнее задание по математике

Похожие статьи:

Математические задачи в сказках с ответами, 5 класс