Математическая игра для 6 класса с ответами

Сценарий игры по математике для учащихся 6 класса. Игра «Математик-банкир»

В игре могут участвовать 2—3 команды, каждая из которых представляет правление банка.

Игроки выбирают президента банка (капитана команды), название банка.

На столе разложены карточки с заданиями в перевернутом виде, каждая карточка имеет стоимость от 50 до 300 у. е. в зависимости от сложности задачи. Это возможные вклады, инвестиции и т. д. Стартовый капитал каждого банка — 500 у. е. Выбрав карточку с заданием и решив задачу (на обдумывание времени дается в зависимости от сложности: 50 у. е. — 1 мин, 100 у. е. — 2 мин, 150 у. е. — 3 мин, 200 у. е. — 4 мин, 300 у. е. — 5 мин), банк пополняет свой капитал на обозначенную сумму. В случае разногласий членов правления окончательное решение принимает президент.

Если банк дает неправильный ответ, то:

а) его капитал уменьшается на стоимость задания, если правильный ответ дает другая команда;

б) капитал уменьшается на 50 процентов стоимости задания, если другая команда также дает неправильный ответ или отказывается отвечать.

Банки могут совершать обоюдовыгодные сделки: продать или купить задание по договорной цене.

Игра заканчивается в связи с банкротством одного из банков (или двух, если играют три команды). Если задания закончились раньше банкротства, то подсчитываются доходы банков и объявляется победитель.

Задания к игре:

1. Найдите дробь, числитель которой меньше знаменателя и которая не изменяется, если ее перевернуть «вверх ногами». (150 у. е.) Ответ: 6/9.

2. Найдите закономерность и запишите следующие два числа в ряду чисел: ½; 2/3; 4/5; 7/8; 11/12;… (50 у.е.)

Ответ: 16/17; 22/23.

3. После того как туристы прошли 1 км и половину оставшегося пути, им ещё осталось пройти треть всего пути и 1 км. Чему равен путь? (300 у. е.)

Ответ: 9 км.

Решение: Пусть весь путь х км. Имеем уравнение:

4. Найдите сумму чисел

0,01 + 0,02 + 0,03 +...+ 0,98 + 0,99. (300 у. е.)

Ответ: 49,5.

Решение: 0,01 + 0,99 = 1; 0,02 + 0,98 = 1 и т. д. Всего 99 слагаемых, 49 пар и одно слагаемое (0,5) без пары. Итого, 49,5.

5. Какой знак нужно поставить между цифрами 4 и 5, чтобы получилось число, большее четырех, но меньшее пяти? (50 у. е.) Ответ: запятую, число 4,5.

6. Масса куриного яйца — 80 г. Белок составляет 55 % всей массы, а желток— 75 % массы белка. Найти массу скорлупы. (100 у. е.)

Ответ: 3 г. Решение: белок: 0,55 • 80 = 44 (г); желток: 0,75 • • 44 = 33 (г); 80 - (44 + 33) = 3 (г).

7. В клетке находятся фазаны и кролики. Известно, что них 35 голов и 94 ноги. Сколько в клетке фазанов и сколько кроликов? (200 у. е.)

Ответ: 23 фазана и 12 кроликов.

Решение: пусть в клетке х фазанов и у кроликов.

Имеем

8. Какой наименьший угол составляют стрелки часов в 2 часа? (50 у. е.)

Ответ: 60°.

9. Малыш подарил Карлсону весы, и тот начал взвешивать игрушки. Машину уравновесили мяч и 2 кубика, а машину с кубиком — 2 мяча. Сколько кубиков уравновесят машину? (200 у. е.) Ответ: машину уравновесят 5 кубиков.

Решение:

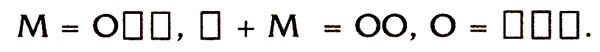
10. Используя все десять цифр, каждую из которых можно применить только раз, запишите возможно меньшее число. (100 у. е.) Ответ: 1023456789.

11. Часы с боем отбивают полные удары каждый час и каждые полчаса — по одному удару. Сколько ударов в сутки отобьют эти часы? (150 у. е.) Ответ: 180 ударов.

12. Восстановите умножение:

13. В доме 100 квартир. Сколько раз на табличке написана цифра «9»? (200 у. е.) Ответ: 20раз.

14. Если в 12 часов ночи идет дождь, то можно ли через 72 часа ожидать солнечную погоду? (150 у. е.) Ответ: нет, будет опять ночь.

15. В велосипедном колесе 20 спиц. А сколько будет промежутков между спицами? (50 у. е) Ответ: 20 промежутков. (Для решения используется идея соответствия. Справа от каждой спицы один промежуток, значит, промежутков столько же, сколько спиц.)

16. Вместо квадратиков поставьте такие дроби, чтобы получилось верное равенство:

Ответ: например,

17. На одну чашку весов положен кусок мыла, на другую – ¾ такого же куска и еще гирька массой 50 г.

Весы оказались в равновесии. Какова масса куска мыла? (200 у. е.) Ответ: 200 г.

Решение: масса куска мыла больше ¾ массы на ¼. Значит ¼, массы куска мыла — это 50 г, тогда масса всего куска — 200 г.

18. Найдите такое целое значение а, чтобы значение выражения (a+9)/(a+6) было целым числом. (50 у. е.)

Ответ: например, —3.

19. Мальчик купил две книги, причем первая на 50 % дороже второй. На сколько процентов вторая книга дешевле первой? (200 у. е.) Ответ: на 33 1/3%.

20. Найдите число, четверть которого равна половине. (50 у. е.) Ответ: 2.

21. Выход муки при размоле пшеницы — 80 %. При выпечке хлеба получается припек в 40 %. С какой площади нужно собрать пшеницу при урожайности 15 u/га, чтобы получить 1 кг пшеничного хлеба? (300 у. е.) Ответ: примерно 6 м2.

Решение: из х г пшеницы получится 0,8 • 1,4х г хлеба. Имеем уравнение 1,12х =1000, х = 892. При урожайности 15 ц/га с 1 м² собирают 150 г зерна. 892:150 = 6.

22. Задуманы два числа. Их сумма равна 60, а частное при делении одного на другое равно 4. Какие числа задуманы? (100 у. е.) Ответ: 12 и 48.

Решение: пусть задуманные числа — х и 4х, тогда х + 4х = 60, х = 12, а 4х = 48.

Математическая игра для 6 класса с ответами

Сценарий игры по математике для учащихся 6 класса. Игра «Математик-банкир»

Задания к игре:

Похожие статьи: